MTシステム問答・応用編⑧
そうですね。しかし、ルールは同じですからプログラムを組めば大丈夫です。現場で使われている問題の中には変数が数百とか数千というものもありますが、コンピュータが計算しますので、全然心配は要りません。
それで、14個の変数について全部の組の相関係数を求めたら、以下の表のようになります。
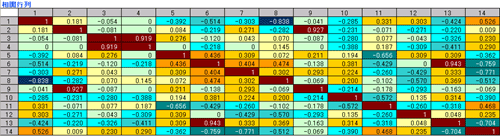
うわあ、なんだこりゃあ!
そんなに驚かないでください。さきほど出てきた14個の特徴の2個ずつのペアの相関係数を求めたらこうなるだけです。さきほどの表の1列目と2列目の相関係数は0.18と言いましたが、それが上の表の1行目と2列目の位置にありますね。1列目と5列目の相関係数は -0.39と言いましたが、1行目と5列目の位置にあります。ほかも全部同じです。

色にびっくりしたこともあるけどね。ああ、汗かいた。
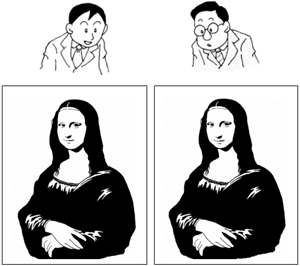
では、とっておきの例で説明しましょう。絵を使いますから、わかりやすいと思います。 下の絵はモナリザの絵ですね。
おっと、次はモナリザか。まあいいや、わかりやすければ。でも、うまい絵だな。誰が描いたの?
札幌に住むデザイナで、子供たちに夢をあげたりもしている人です。
ふーん。札幌に住んでいるのか。時計台、ポプラ並木・・・素敵な街だ。 ところで、左の絵はよく見るモナリザだけど、右の絵はどこかがおかしくない?
おかしいと感じるでしょう。実は、右の絵では目も鼻も口も、皆大きさと形は同じですが、位置関係が異なっています。
ああ、本当だ。えーと、鼻と口が下にずれていて、目の間隔も広いね。そうか、相対関係が違う例だと言いたいんだね?目、鼻、口となると3つあることになる。
そうですね。両目の間隔も含めると4つの相対関係ということになります。人間は相手が誰かを認識するときに、目鼻の形という情報も使いますが、それらの相対関係という情報も使っていますね。この場合、相対関係が大変重要なことがよくわかります。
