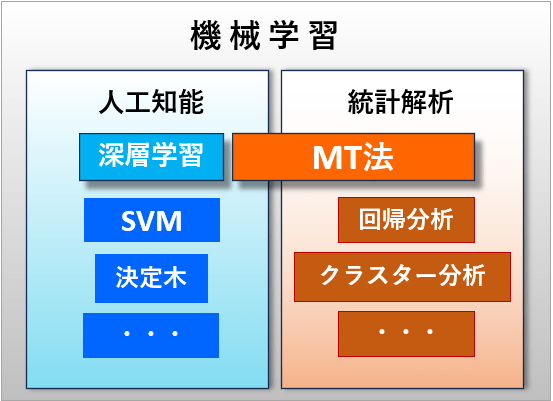
機械学習におけるMT法と深層学習の違い
機械学習の定義
機械学習という言葉は1950年代に初めて使われました。その当時は、統計解析などの計算もすべて機械学習の一部と考えられていました。また、人工知能(AI)という言葉も同じ頃に登場しました。
1980年代には、神経回路を模したニューラルネットワーク(ANN)が注目されました。しかし、技術的な制約があり、そのために一時的にブームが終わりました。
1995年には、MTシステム(MT法)が提案されました。これは、統計学を使って認識や予測を行う技術で、AIの用途とも重なります。MT法の特徴は、正常な状態のみを学習する点にあります。
2000年代に入ると、深層学習が登場し、ニューラルネットワークの層数を増やすことができるようになりました。特にオートエンコーダ型のニューラルネットワークが、この層数の拡張に重要な役割を果たしました。MT法の「正常状態のみを学習する」という考え方が、この深層学習の発展に影響を与えた可能性があります。
ものづくりにおける両者の特性(MT法の利点)
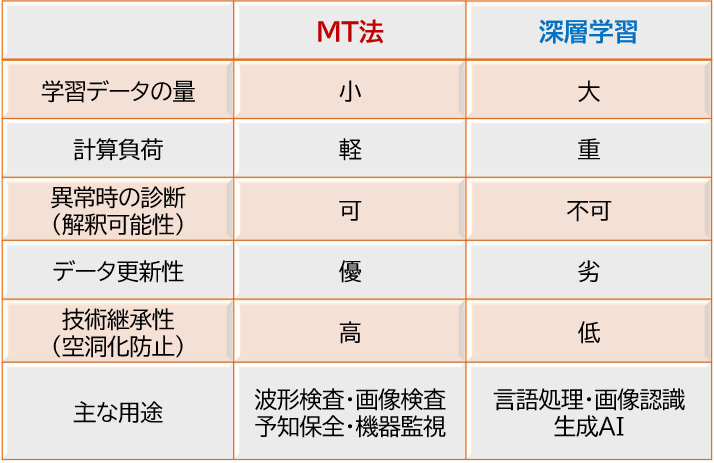
機械学習を製造プロセスの監視や製品検査などで利用する場合には、以下事項が重要となります。
・学習データ量:学習(教師)データが少ないこと
・計算負荷:処理のリアルタイム性、少ないメモリでの処理
・異常時の診断:技術者に分かり、的確な診断
・データ更新性: 新たなデータを即時に取り込めること
・技術継承性:次世代技術者への引継ぎが容易なこと
MT法はものづくりや監視で重要となる、これら事項について優れた能力を有しています。
適用領域
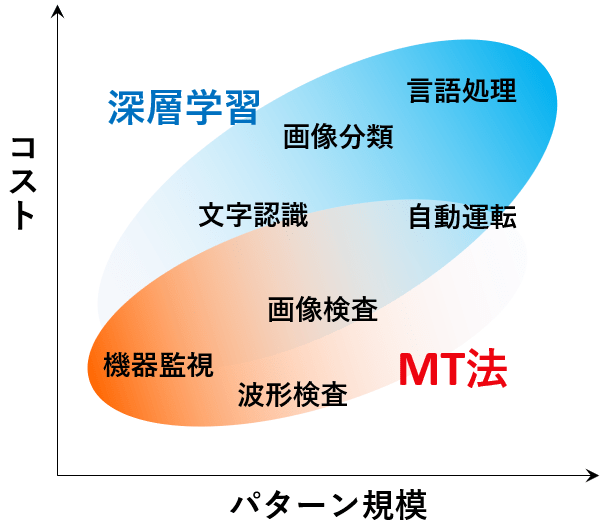
MT法とディープラーニングは、それぞれ異なる強みを持っています。
MT法の強み
- 製造業や品質管理で異常を検知し、プロセスを最適化するのに適しています。
- 少ないデータでも高精度な判定や予測が可能です。
- 技術者が特徴量を把握できるため、異常や不良品が発生した際に即時対応できます。
ディープラーニングの強み
- 大量のデータを扱うのが得意です。
- 特に画像、音声、テキストなどの複雑なデータに対して高精度な予測や分類ができます。
- 変化するデータにも柔軟に対応でき、動的な環境での使用に適しています。
特徴量はネットワーク内部で自動的に形成されますが、過程や結果がブラックボックス化し、技術者が制御できないという不便さもあります。
構造の違い
 MT法の構造
MT法の構造
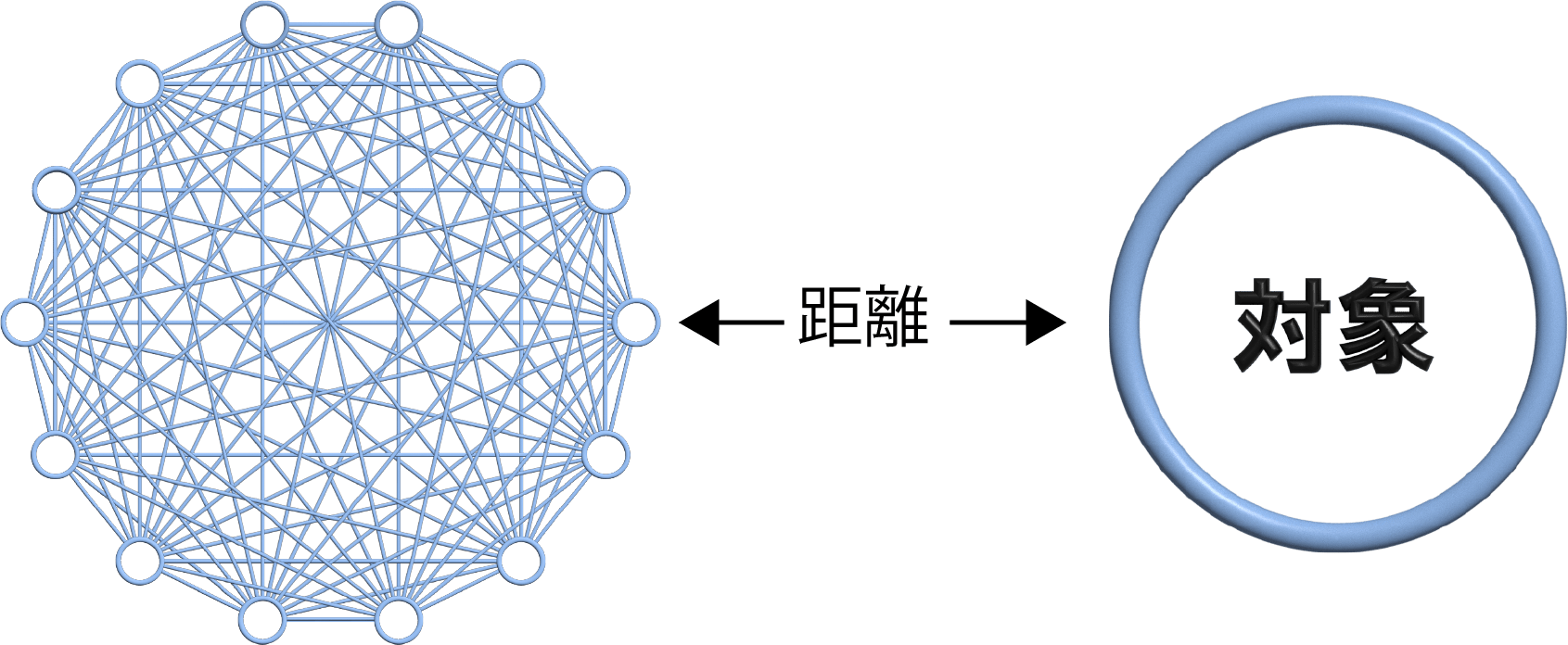 正常からの距離
正常からの距離
MT法の構造
MT法は、左図のようなネットワーク構造を持っています。〇は項目を示し、線は項目間の相関を表しています。MT法はこの構造を利用して、パターンの違いを見分けます。相関とは、2つの項目間の関係の強さのことです。例えば、蛇口の開度と水量には強い相関があります。この相関係数は、すべての項目間で計算できます。
この相関ネットワークは、正常データのみを使って作られます。そして、このネットワークから対象までの距離を計算します。もし距離が遠ければ、その対象は正常なパターンとは異なる、つまり異常であることを意味します。これにより、MT法は未知の異常も検出できるのです。
距離の計算にはマハラノビス距離が使われます。一般的には、距離が4を超えると異常と判定されます。つまり、距離が4より大きければ、その対象が正常である確率が低いということです。
MT法の構造は、学習データに対して一種類しかありませんが、深層学習には様々な構造があります。MT法のシンプルな構造により、少ないメモリで高速に計算できるのが特徴です。
 深層学習の構造
深層学習の構造
(オートエンコーダの場合)
深層学習の構造
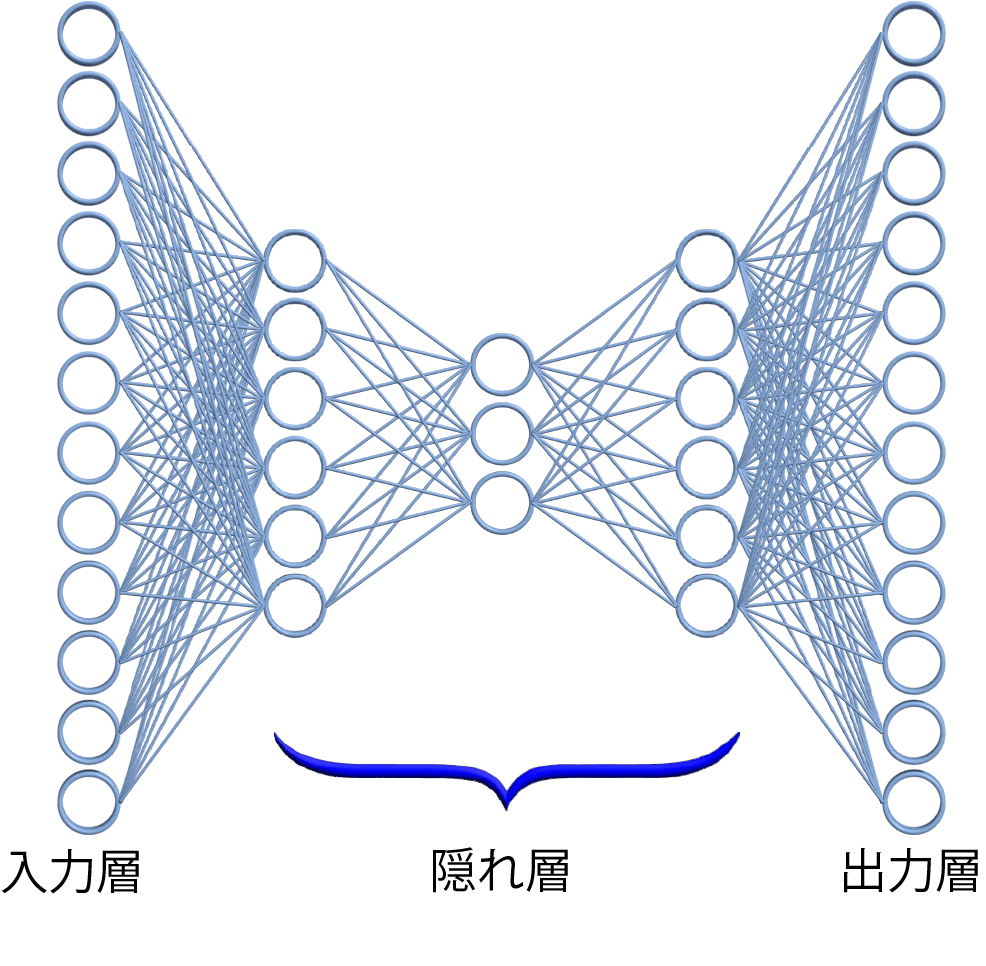
深層学習は、入力層、隠れ層、出力層からなる構造を持っています。〇は人間の脳細胞、直線は細胞間の結合強度を示します。入力層と出力層に「教師データ」と呼ばれる既知のデータを与え、数千回から数万回の繰り返し学習により、結合強度が調整されます。左図の構造では、MT法と同様に正常データのみを学習することができ、この構造はオートエンコーダと呼ばれます。
学習したパターンと類似したパターンが入力されると、出力層に現れる誤差が小さくなり、類似していないパターンでは誤差が大きくなります。誤差の総和が小さければ、そのパターンは正常に近いと判定されます。
隠れ層の数や細胞の数は、利用者が自由に設定できます。例えば、隠れ層の数を10層や100層にすることも、細胞(〇)の数を任意に増やすことも可能です。構造の規模が大きくなるほど、学習できるパターンの数も増えます。

MT法:ホワイトボックス

深層学習:ブラックボックス
ホワイトボックスとブラックボックス
MT法では異常が発生した場合に明示的な原因診断を行うことができます。どの項目が正常と異なっていたのか、あるいはバランスを崩していたかが明らかになります。ですから、ホワイトボックス型AIと呼ばれています。これに対して深層学習では、技術者が解釈しやすい診断結果を提示することが不得意です。ブラックボックスと言われる理由の一つです。賢いのですが、コミュニケーション能力に難があるといえます。
この相違は、ネットワーク構造に起因します。私たちは相関を理解していますから、異常時の診断結果も理解しやすいのです。これに対して深層学習は脳の構造を模擬しており、学習時には誤差が収束するように計算が進みます。収束した結果や判定結果がどのような意味を持つかを解明・解釈することは、現時点では有効な手立てがありません。
特性の違い
学習データ
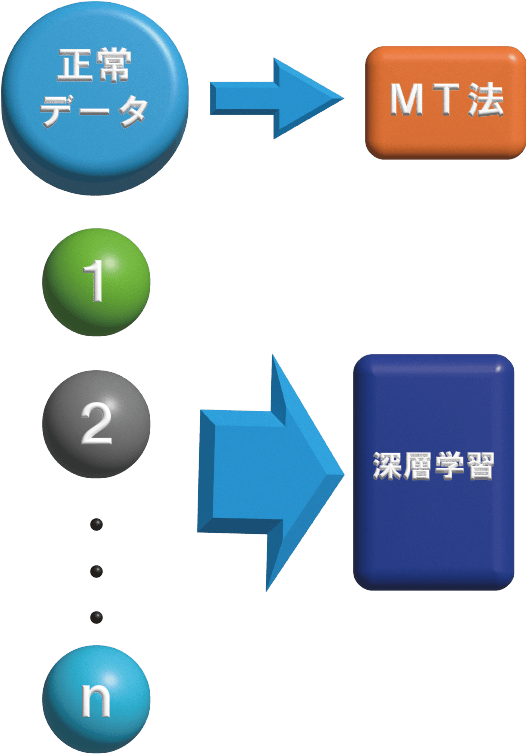
MT法は正常状態だけを学習し、深層学習は多くの場合で複数の状態を学習します。
ものづくりの現場では、正常データは数多く存在しますが、異常は少なく、めったにないことさえあり、未知の異常もあるはずです。つまり、異常を網羅することは不可能と言えます。そのため、”正常以外”に反応するMT法の考え方は、ものづくりの場面では合理的です。学習に準備するデータも少なくて済みます。
深層学習は一般に、一つのネットワークが多くのパターンを学習します。そのため、画像・文字・言語などの分類問題で威力を発揮します。深層学習でも正常なデータだけを学習する構造があります。しかしネットワーク規模は大きく、計算負荷はMT法より相当に大きくなります。
計算速度
MT法と深層学習とはネットワークの規模が違いますので、簡素なMT法の方が計算速度は高速です。特に学習速度は、100倍、1000倍(*)異なります。
用途が正常/異常の判定だとするなら、MT法の方が高速ですし、原因診断の計算もリアルタイムで可能です。以下は、パソコン(intel core i7)による計算速度の例です。
・学習時間(1,000項目×3,000サンプル) : 2.0 秒
・マハラノビス距離計算時間(1,000項目) : 0.002秒
(*)MT法は項目数で計算量がほぼ定まりますが、深層学習はネットワークの規模が任意ですので、計算量は幅があります。最も簡素な構造でも学習時の計算量はMT法の100倍以上になります。
異常への感度
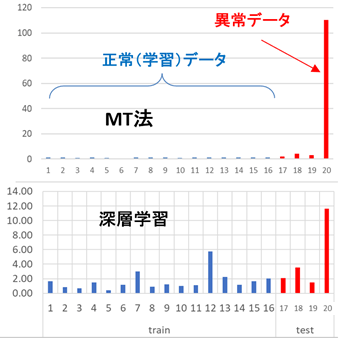
ものづくりで最も重要なことは「異常を明瞭に検出すること」です。左図は文字パターンの認識結果で、1~16が学習データ、17~20が未知データです。未知データの中で、17~19は正常、20は異常パターンです。
MT法(上のグラフ)では、学習データの距離(異常の程度)はおしなべて小さく、異常パターンでは極端に大きくなっています。これに対して深層学習では、正常と異常は判別していますが、異常の場合の数値はそれほど大きくはありません。
異常への感度という点では、MT法のほうが優れていることが多いようです。これは、MT法が正常状態のみを学習し、構造が簡素であるためと考えられます。
異常原因の診断
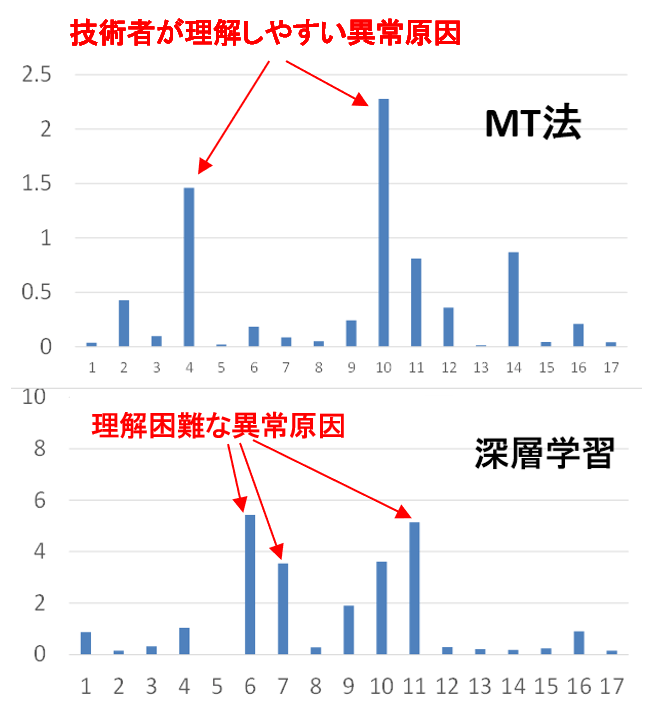
左の二つの棒グラフは、MT法および深層学習の異常診断の結果です。横軸がデータの項目番号で、どちらも同じ異常データでの結果です。
MT法では項目4と10が大きな原因であることを示しています。実際に、この二つは異常原因として理解できる項目です。深層学習では4つの項目が大きくなっていますが、人間には理解は容易ではありません。MT法は相関を利用したシンプルな数理なのに対し、深層学習では人間の理解を越えた”特別な脳”が学習したためです。
人間に理解容易な原因診断ができれば、異常対応も容易になりますので、MT法の方が有利といえます。
補足
特徴化技術
MT法では特徴化技術も提供されていますが、それらを組み合わせることで深層学習と同じことができることがしばしばあります。特に画像検査や時系列波形の問題です。
深層学習というブラックボックスに委ねる方が技術者の負担が小さい面もありますが、技術者がプロセスを理解しながら利用できるMT法の方が、中長期的には技術の継続性を保つことができます。