MT法(Mahalanobis-Taguchi method)
正常度の物差し
MT法は正常データを基準としたときに、対象が基準内にあるかどうかを数値化する方法です。つまり、正常度のものさしを作るという考え方を適用しています。正常データ群のことを“単位空間”と呼びます。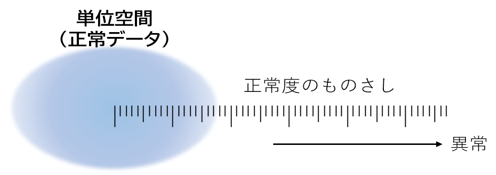
図では対象の位置がものさしの右側に行くほど、異常の程度が大きいことを示します。たとえば、対象の値が2~3程度であれば正常ですが、もっと大きな値(たとえば10)であれば異常と判断されます。
ものづくりの現場などでは正常データの取得は容易ですが、異常データの取得は一般に困難ですし、未知の異常もあります。
MT法の考え方はシンプルですが異常検出感度が高く、機器・設備の監視や予知保全、推移予測、あるいは検査問題に適しています。
文字認識の例
MT法の考え方はシンプルでありながら、私たち人間の感覚と近い結果を得ることができます。その例をご紹介します。
以下の図は、MT法による文字認識の例です。左側の16個のパターンは、数字に限ればいずれも”5”と読むことができます。これらを基準(単位空間)として、右側の4個のパターンのマハラノビス距離を求めると、それぞれ 1.8 3.2 4.1 110.1 となります。距離が大きいほど、基準としたデータと異なることを意味します。
しきい値を5程度とすると、はじめの3つは5と認識され、4つ目は5と認識できないことになります。このように、人間の認識と近い結果を容易に得ることができます。

説明可能なAI(XAI)
MT法では判定結果が異常となった場合、原因診断を実行することができます。品質工学で利用する直交表とSN比を利用する方法や、貢献度法という数理を適用します。深層学習(ディープ・ラーニング)では原因診断ができないことが大きな課題ですので、MT法の利点の一つと言えます。異常原因のわかるAIは「説明可能なAI = Explainable AI (XAI)」、あるいはホワイトボックス型AIと呼ばれます。
名称の変遷
田口玄一博士は、1995年にMTSを発表しました。これは Mahalanobis-Taguchi System の略で、現在のMT法のことです。しかし、田口博士からはそれ以降さまざまな解析数理が発表され、それらを総称してMT(マハラノビス・タグチ)システムと呼ぶことになりました。結果の精度や項目数とサンプル数の課題など、それまでに存在していた分析・解析技術の課題を克服する理論として、品質工学会以外からも評価・注目されています。
提案された主な数理として、T法(1)・T法(2)・T法(3)=RT法・標準化誤圧法・MTA法などがあります。そしてさらに、Schmidtの数理を導入した Mahalanobis-Taguchi-Shmidt という数理も提案され、これをMTSと呼称する場合もあります。
このように新たな計算手法が次々と提案され、名称が変遷してきたと言えます。現時点で事例が多く、実用的な観点で重要な技術として、MT法・RT法・標準化誤圧法・T法(1)・MSRを挙げることができます。
二つの基礎事項
MT法は、以下二つのことが基礎になっています。
(1)相関を利用する
(2)正常群を基準とする
相関
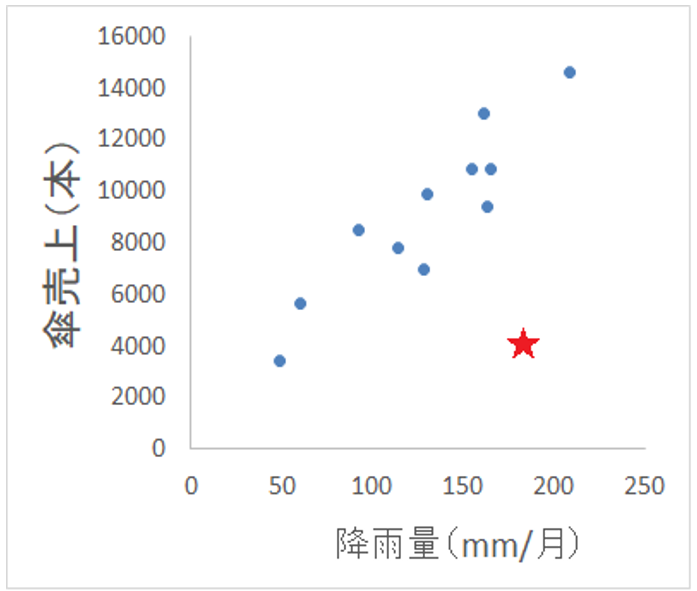
「相関」とは、2つの変数間の関連性の強さです。たとえば下図の12個の●は降雨量と傘売上数の10年間の平均的散布図ですが、雨の多い時期は傘がたくさん売れますので、両者には強い(高い)相関があります。しかし、★のように降雨量が多いのに傘売上が少ないとすると、なんらかの「いつもとは違う状況が起きた」と考えられます。
MT法の数理は相関の強さ、すなわち相関係数を利用します。相関係数は全ての2変数間で計算されます。図に相関係数rの大きさと、2変数間のおおよその関係を楕円で示します。相関がゼロであれば円ですが、相関が強くなると細い楕円になり、相関が1であれば楕円が完全につぶれて直線となります。負の相関では、楕円は右下がりになります。

正常群による基準(単位空間)
二番目の「正常群を基準とする」とは、たとえば健康な人々のデータ(変数)はとりうる範囲も相関関係も一様なので、パターンの基準になるという意味です。正常状態や良品のばらつきは小さく、反対に異常や不良品にはさまざまな種類や程度があります。MT法では正常群だけで認識空間(単位空間)を作りますので、未知・未経験の不具合も検知することができます。
MT法では相関は計算で求めますが、正常群は人が決めるテーマです。たとえば、熟練検査員が良品と判定した製品を正常群とします。そのため、MT法は人間の判断を再現するという特質を持っており、技術伝承の場面でも利用されています。
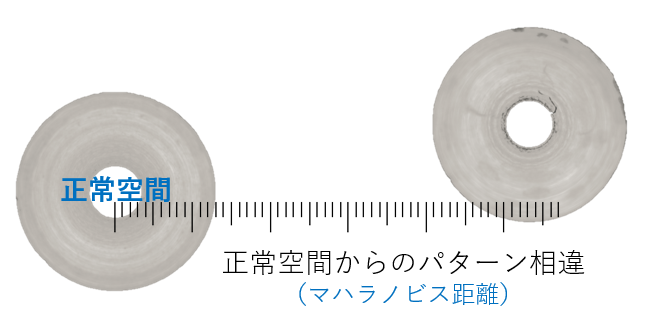
マハラノビス距離の計算式
以下にマハラノビス距離D2の計算式を記載します。詳細は割愛しますが、この式の働きは前述の楕円を幾何学的な変換でいったん円に戻し、ユークリッド距離を求めることです。式中のkは変数の数、Yは対象データの規準化後のベクトル、ɑは相関係数行列の逆行列の成分です。
なお、マハラノビス距離を求めるために主成分分析や直交展開の式などを使用する方法もあります。計算を途中で止めずに全ての成分について計算すると、値は一致します。
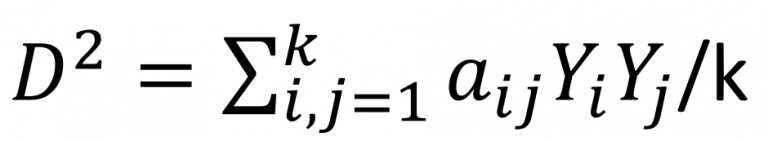
多重共線性
マハラノビス距離の計算過程には、実は実用上の課題があります。相関係数が±1となった場合に計算ができないという課題です。計算過程にゼロ割りが発生するからです。この状態を多重共線性(multi-colinearity)いいます。
しかし現実の問題では、相関係数が1となることはよくあります。たとえば、流量を計測する場合、センサーを2か所に設置すると同じ値を示します。すなわち、途中に漏れなどがない正常な状態では、相関係数は1となります。しかし一方を外してしまうと、異常の検知ができないため、2つのセンサーはどうしても必要になります。
したがって、多重共線性がある場合でも計算が可能とする必要になります。アングルトライのMT法は、多重共線性がある場合でも計算が可能となる対策が施されています。
どの項目で異常かが分かる
MT法では、マハラノビス距離が大きくなった場合の原因診断が可能です。すなわちどの変数が、あるいはどの変数の組み合わせが異常原因なのかを知ることができます。深層学習の場合、現状では構造上の理由から診断ができません。異常理由を説明できるAIを「説明可能なAI (Explainable AI : XAI)」と呼びますので、MT法はXAIの一つと言えます。
下のグラフは、健康データの原因診断結果です。17項目で健康かどうかを判定した結果、マハラノビス距離=49 と大きく、健康ではないと判定されました。そして6番目と7番目の項目が異常に大きく寄与しており、受診者は肝臓疾患が疑われます。
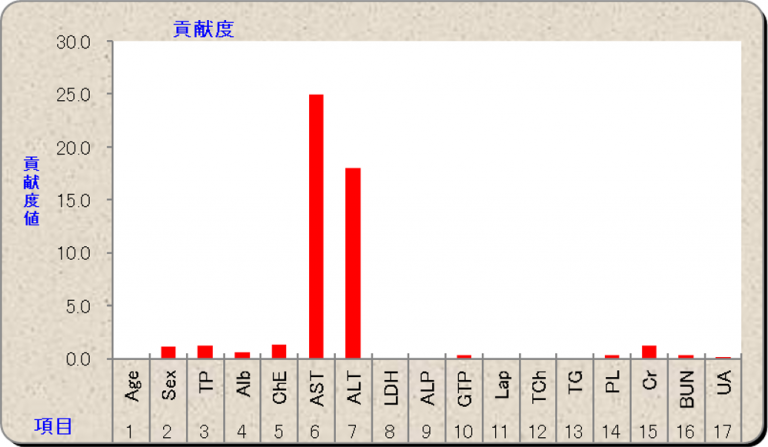
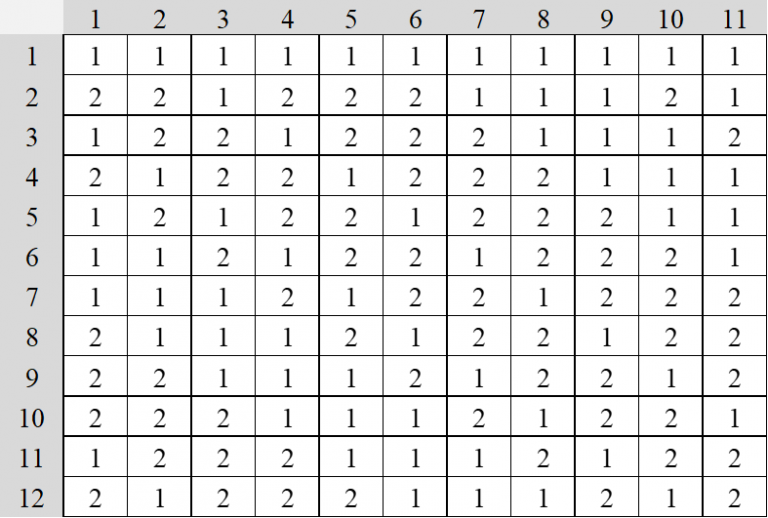
診断は、品質工学における2水準系直交表(多くはPaley型)とSN比を利用します。以下の表はPaley型直交表の例です。なお、アングルトライのソフトウェアでは、直交表方式より1,000倍以上高速な“貢献度法”を利用することもできます。
処理速度
MT法は計算量が少なく(深層学習の1/1,000以下)、処理は非常に高速です。
弊社ソフトウェアの処理時間は以下の通りです(intel CORE i7利用時)。
単位空間計算時間(1,000項目×3,000サンプル) : 2.0 秒
マハラノビス距離計算時間(1,000項目) : 0.002秒
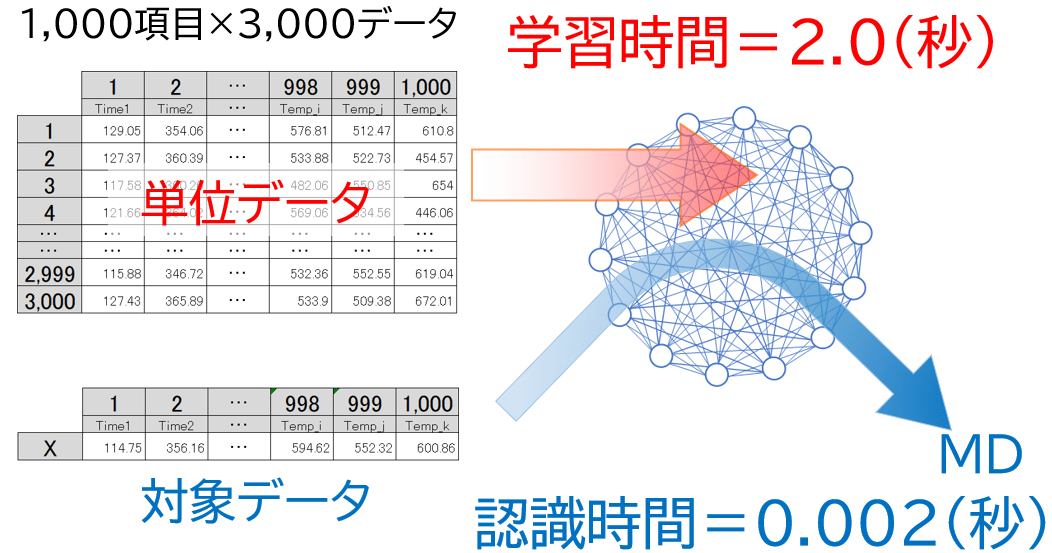
計算に要するメモリ等の計算負荷が小さく、現場の端末で判断処理するエッジ・コンピューティングの用途にも適しています。ものづくりやインフラを対象とした検査・監視、あるいは予防保全などでも利用されています。
弊社のソフトウェアは処理時間のほか、計算精度の確保や計算不能の回避処理を持ち、どのようなデータセットについても高い認識精度を実現しています。
応用分野
MTシステムの応用分野(実績)の例を以下一覧に示します。
| 分野 | 事 例 |
| 検査 | ・ギヤ・ポンプの異音検査 ・半導体・リチウムイオン電池画像検査 ・外観検査(自動車部品・シート部品) ・漢方薬素材のクロマトグラム検査 ・圧入・圧着 |
| 予知保全 | ・機械の故障予測 ・水質浄化能力の劣化予測 ・電力消費予測 ・鉄塔などインフラの劣化診断 |
| 工程最適化 | ・液晶パネル用膜部品の工程制御 ・ダイキャスト・樹脂成型の工程安定化 |
