MTシステム問答・応用編⑦
ふーん。そうすると、さきほどの点Cの距離はどうなるんだい?
数式に基づいて計算すると、約10になります(*)。元になった12個の点やBは皆距離が0から2程度ですから、Cは仲間とは言えないことが分ります。
(*)ここでは二乗の距離で解説しています。詳しくは後で解説します。
「数式に基づいて説明すると」か。難しくなければ説明してよ。
相関係数を利用して、仲間の程度、つまり距離がうまく定義できる数式で、この数式から求められる距離を、「マハラノビス距離」と言います。数式を考案したのがインドの数学者マハラノビス博士なので、そう呼ばれています。
インドでは、いろいろの動物の骨が出土するのですが、骨の特徴を用いてうまく分類する方法がないかと考えた末に、距離の導き方を発見したのです。

マハラノビスさんか。言いにくいな。その自動車殿堂入りをされた田口博士は、マハラノビスさんの数式が仲間の程度を扱うことに適用できると考えたわけかい?
そうです。実は、田口博士とマハラノビス博士はきわめて親しいお付き合いがあったのです。マハラノビス博士は私財を投げ打って、カルカッタにインド統計研究所を設立されました。そして、田口博士がこの研究所に客員教授として招かれて以来、親交があったそうです。
なるほど。お二人のマハラノビス距離は近かったんだ。仲間であり友人であり・・・そんな出会いがあったの。
ときどき、すごいこと言いますね。
出会いだけなら我々にもありますが、その出会いからすごいものを残すところが偉い方々の素晴らしいところです。
ところで、さっきから少し考えていたんだけど、降水量と傘の売上は2つの関係だけだろう? ところが、文字の場合には変化の箇所やら石の数やらがたくさんあるよね。確か14種類あったはずだ。こんな場合、その相関係数とやらはどうなるの?
2つだけの関係は"2次元"ですね。もっと多くの場合は"多次元"と呼びます。多次元は、2次元の関係の集まりですよね。つまり、全ての2つの組ごとに相関を求めれば良いわけです。
うーん。つまりこういうことかい?
多次元であっても、2つずつのペアで相関係数を計算するといい。合ってる?
そうです。その通りです。
前に出てきた5という文字から取り出した14個の値を改めて見直してみます。
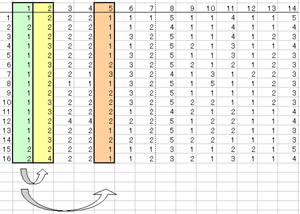
だけど、14個もあると全部のペアの数ってかなりの数になるね。
